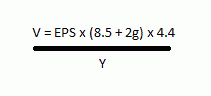In an earlier post (Intrinsic value and a formula) I had a look at a formula proposed by Ben Graham to simplify the mathematical models that were popular at the time. Subsequently, however, after interest rates took off in the 1970s, he returned to this formula and attempted to factor these into the calculation.
The revised formula he created is usually quoted as:
Where:
V = Intrinsic Value
EPS = Current (Normal) Earnings
2g = Twice the expected annual growth rate. Taken from Morningstar’s 5- year analyst estimates, reduced by 25% to be conservative/sensible.
4.4 = the average yield of high-grade corporate bonds in 1962, when the formula was put together
Y = the current yield on AAA corporate bonds. I will use 5.5, which is higher than the current ten-year yield (3.04%). My reason is that, as I am buying for the long-term, I would like to use a more normal yield on the assumption that the yield will return to a long-term average.
This formula still does not take account of the company’s financial structure and debt position, and must only be a starting point, but if it helps me to weed out blatantly over-priced shares then that is a good thing.
It is difficult to know what Graham himself says about this formula, because he produced it after writing the Intelligent Investor. Looking online, I can find the following comment regarding the problem that it does not take debt into consideration: “I see no satisfactory way of reducing the multiplier to avoid attempting a formal valuation of such companies [highly indebted]. In other words, limit your appraisals to enterprises of investment quality, excluding from that category such as do not meet the specific criteria of financial strength.” Graham’s definition of financial strength, incidentally, is very strict; I would expect a very high number of FTSE 100 companies would fail. I might return to this in future.
Additionally, regarding application of this formula and his famed margin of safety: “Also I should require that the buy decisions based on this approach involve a margin of safety factor. This might well be a purchase price not over two-thirds of the central appraised value.”
Application
So, as in my previous post on this subject, I will try to apply this to IBM and Diageo (both of which I am currently purchasing), and throw in Altria, which is another I suspect of being reasonably priced.
Altria Value: (2.26 X (8.5 + (2 X 4.8)) X 4.4) / 5.5 = $32.72
Altria Current Price: $39.11
RGV: 0.84 (see Intrinsic value and a formula for an explanation)
Verdict: Overvalued. So much for my suspicion…
Diageo Value: (104.4 X (8.5 + (2 X 4.5)) X 4.4) / 5.5 = £1461.6
Diageo Current Price: 1807p
Diageo RGV: .81
Verdict: Overvalued as well.
IBM Value: (14.94 X (8.5 + (2 X 6.6)) X 4.4) / 5.5 = $259.36
IBM Current Price: $189.63
IBM RGV: 1.37
Verdict: Still in the hitting zone
I would love to hear from anyone better qualified to evaluate this formula. Is it still useful and, if so, how useful?
References:
- Wikipedia
- All quotes from Common Sense Investing: The Papers of Benjamin Graham 1974, available online courtesy of Redfield, Blonsky & Co., LLC
Disclosure: Long MO, DGE, IBM
Disclaimer: This post is not a recommendation to either buy or sell. Please consult your investment advisor.